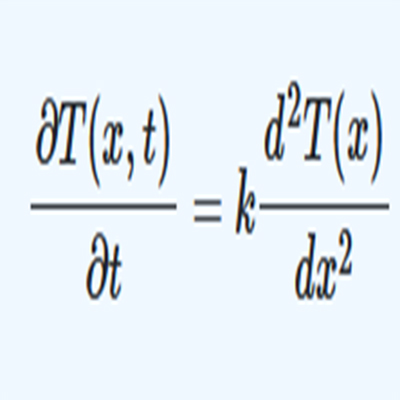Algebraic formulation
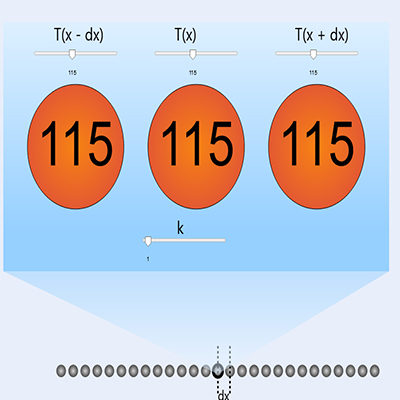
From Newton's law of cooling, $$ \frac{\partial T(x,t)}{\partial t} \propto [T(x+dx,t) - T(x,t)] + [T(x-dx,t) - T(x,t)] $$
Implies,
$$ \frac{\partial T(x,t)}{\partial t} = k_1[T(x+dx,t) - 2T(x,t) + T(x-dx,t)] $$
From calculus we have(click to expand),
\( \therefore \) $$ \frac{\partial T(x,t)}{\partial t} = k_1(dx^2)\frac{\partial ^2 T(x)}{\partial x^2} $$
$$ \frac{\partial T(x,t)}{\partial t} = k\frac{\partial ^2 T(x)}{\partial x^2}$$
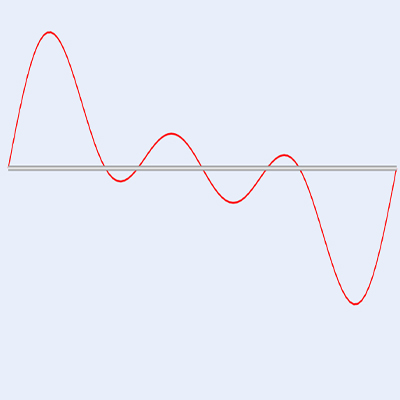
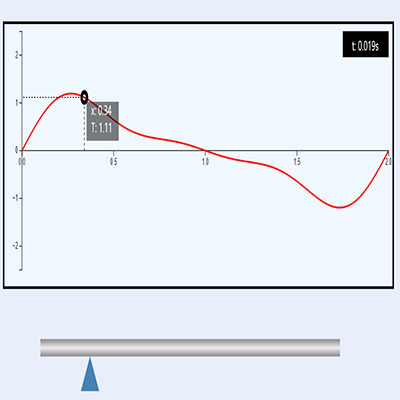
Drag slider derive to heat equation!
$$ \frac{dT}{dx} = \frac{T(x+dx) - T(x)}{dx} $$
$$ \frac{d^2T}{dx^2} = \frac{(\frac{dT}{dx})_{x+dx} - (\frac{dT}{dx})_{x}}{dx} $$
$$ = \frac{(\frac{T(x+2dx) - T(x+dx)}{dx}) - (\frac{T(x+dx) - T(x)}{dx})}{dx} $$
$$ = \frac{T(x+2dx) - 2T(x+dx) + T(x)}{(dx)^2} $$
Putting \(x = x+dx\),
$$ \frac{d^2T}{dx^2} = \frac{T(x+dx) - 2T(x) + T(x-dx)}{(dx)^2} $$
$$ \therefore T(x+dx) - 2T(x) + T(x-dx) = (dx^2)\frac{d^2 T(x,t)}{dx^2} $$