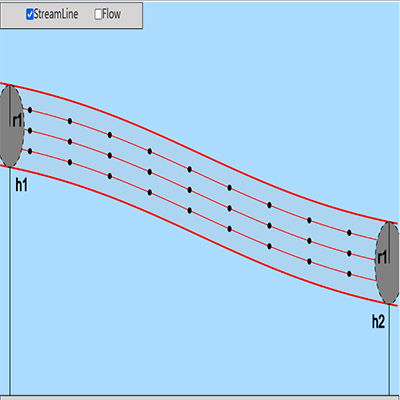
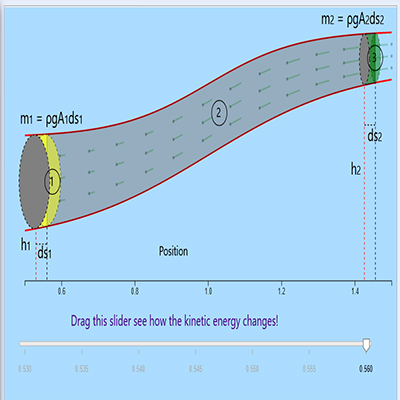
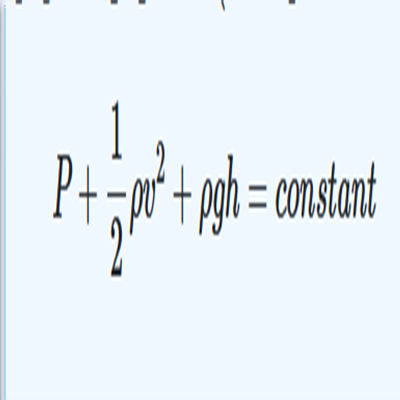Arriving at the final equation
Now we feed the details of our analysis into $$ dW = dK + dU $$
Implies,
$$ P_1A_1ds_1 - P_2A_2ds_2 = (\frac{1}{2}\rho v^2_2ds_2A_2 - \frac{1}{2}\rho v^2_1ds_1A_1)
+ (\rho gh_2ds_2A_2 - \rho gh_1ds_1A_1) $$
$$ (P_1 + \frac{1}{2}\rho v^2_1 + \rho gh_1)ds_1A_1 =
(P_2 + \frac{1}{2}\rho v^2_2 + \rho gh_2)ds_2A_2 $$
\( \text{Since,} \) $$ ds_1A_1 = ds_2A_2 = dV \text{ (incompressible fluid)} $$
$$ P + \frac{1}{2}\rho v^2 + \rho gh = constant $$
Drag slider derive to Bernoulli equation!