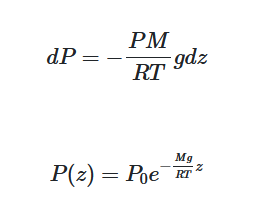$$ PV = nRT $$ $$ V = \frac{m}{\rho} \text{ , } n = \frac{m}{M} $$ $$ \text{where, } \rho = \text{ density },M = \text{ Average molar mass} $$ $$ \therefore \rho = \frac{PM}{RT} $$

$$ dP = -\frac{PM}{RT}gdz $$ $$ \int \frac{dP}{P} = -\frac{Mg}{RT}\int dz $$ $$ \ln (\frac{P}{P_0}) = -\frac{Mg}{RT}z $$ $$ \frac{P}{P_0} = e^{-\frac{Mg}{RT}z} $$